Backpropagation Neural Network

This is an example of a simple symbol recognition problem with three letters T, G and F, in an original form and in a shifted form. The 6 input vectors $x_1, x_2, x_3, x_4, x_5, x_6$ and the corresponding target vectors $d_1, d_2, d_3$ in the training set are:

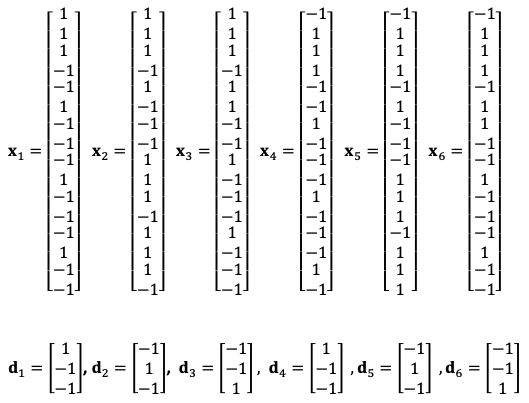
We will assume that the network has one hidden layer with 3 neurons and all continuous perceptrons use the bipolar activation function $f(v)=\frac{1-e^{-v}}{1+e^{-v}}$. Note that the trained network should have 17 input nodes, 3 hidden neurons, and 3 output neurons due to necessary augmentation of inputs and hidden layer by one fixed input. We will assign −1 to all augmented inputs. The resulting network has the following form:

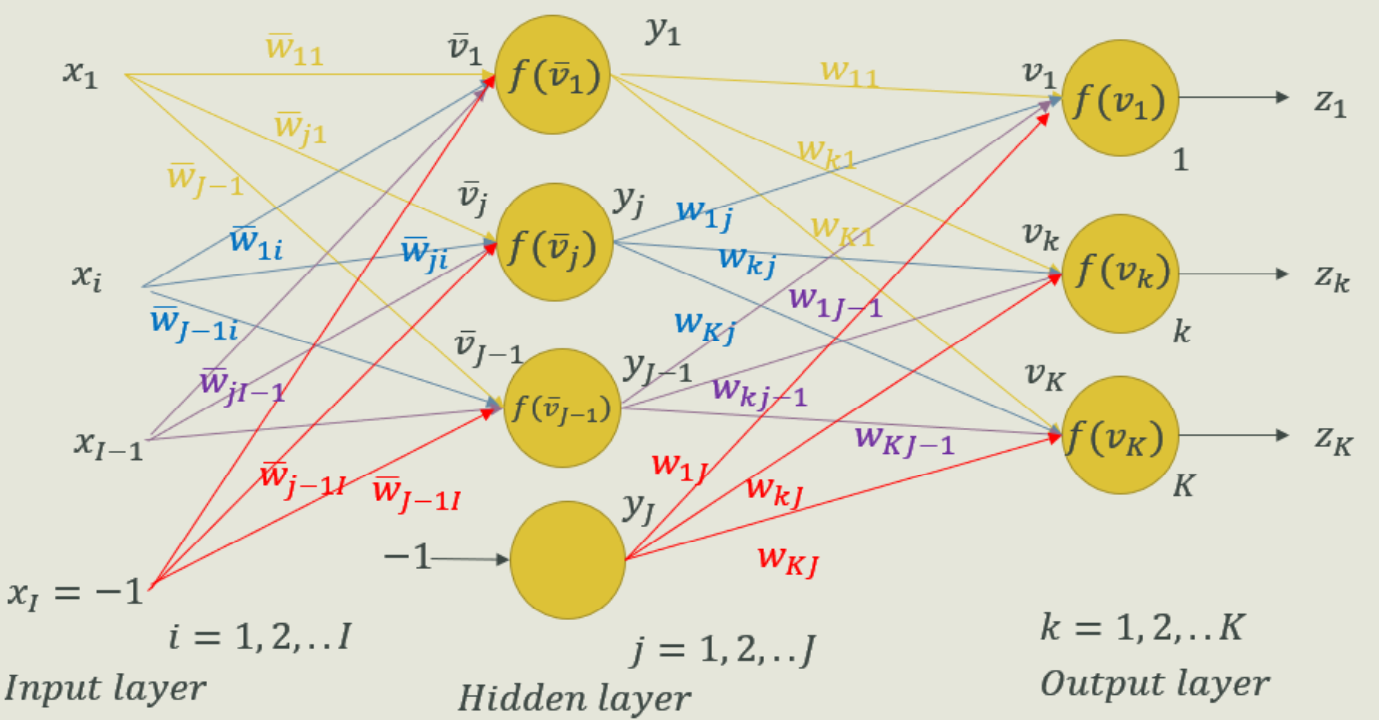
The learning constant $n = 0.25$, and the initial random weights for the output and hidden layers are:

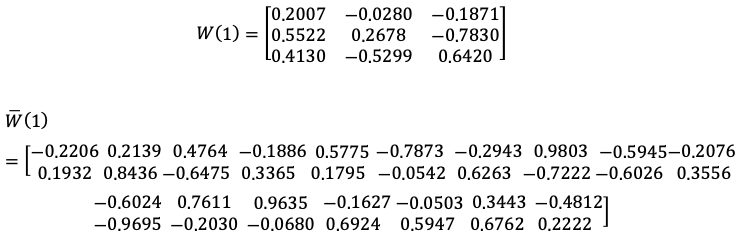
Setup

import numpy as np
import matplotlib.pyplot as plt

# Constants
## input vectors
x_fig = np.array([[1,1,1,-1,-1,1,-1,-1,-1,1,-1,-1,-1,1,-1,-1],
              [1,1,1,-1,1,-1,-1,-1,1,1,1,-1,1,1,1,-1],
              [1,1,1,-1,1,1,-1,-1,1,-1,-1,-1,1,-1,-1,-1],
              [-1,1,1,1,-1,-1,1,-1,-1,-1,1,-1,-1,-1,1,-1],
              [-1,1,1,1,-1,1,-1,-1,-1,1,1,1,-1,1,1,1],
              [-1,1,1,1,-1,1,1,-1,-1,1,-1,-1,-1,1,-1,-1]])

x = np.append(x_fig, -1*np.ones((6,1)), axis=1)

## Target vectors
d = np.array([[1,-1,-1],
              [-1,1,-1],
              [-1,-1,1],
              [1,-1,-1],
              [-1,1,-1],
              [-1,-1,1]])

## Learning rate
n = 0.25

# Visualize the data
# plt.figure(figsize=(6, 6))
for i in range(6):
    ax = plt.subplot(2, 3, i + 1)
    plt.imshow(x_fig[i].reshape(4,4))
    plt.title(str(d[i]))
    plt.axis("off")
plt.show()

# Variables
## Initial random output layer weight matrix W1
w = np.array([[0.2007, -0.0280, -0.1871],
              [0.5522, 0.2678, -0.7830],
              [0.4130, -0.5299, 0.6420]])

## Initial hidden layer weight matrix W_1
wp = np.array([[-0.2206, 0.2139, 0.4764, -0.1886, 0.5775, -0.7873, 
                 -0.2943, 0.9803, -0.5945, -0.2076, -0.6024, 0.7611, 
                 0.9635, -0.1627, -0.0503, 0.3443, -0.4812],
                [0.1932, 0.8436, -0.6475, 0.3365, 0.1795, -0.0542, 
                 0.6263, -0.7222, -0.6026, 0.3556, -0.9695, -0.2030,
                 -0.0680, 0.6924, 0.5947, 0.6762, 0.2222]])

# activation function and derivative of the activation function
## Bipolar function
def bipolar(v):
    return ((1-np.exp(-v))/(1+np.exp(-v)))

## Derivative of the bipolar function
def dbipolar(v):
    return 0.5*(1-v**2)

Solution

# Multilayer Neural Network:
## Initial output layer weight matrix W
w = np.array([[0.2007, -0.0280, -0.1871],
              [0.5522, 0.2678, -0.7830],
              [0.4130, -0.5299, 0.6420]])

## Initial hidden layer weight matrix W_1
wp = np.array([[-0.2206, 0.2139, 0.4764, -0.1886, 0.5775, -0.7873, 
                 -0.2943, 0.9803, -0.5945, -0.2076, -0.6024, 0.7611, 
                 0.9635, -0.1627, -0.0503, 0.3443, -0.4812],
                [0.1932, 0.8436, -0.6475, 0.3365, 0.1795, -0.0542, 
                 0.6263, -0.7222, -0.6026, 0.3556, -0.9695, -0.2030,
                 -0.0680, 0.6924, 0.5947, 0.6762, 0.2222]])
wh = [w]
wph = [wp]
cr = []
for j in range(200):
    e = 0
    for i in range(len(x)):
        # Hidden layer
        vp = np.dot(wp, x[i])
        y = bipolar(vp)
        dy = dbipolar(y)
        
        # Output layer    
        v = np.dot(w, np.append(y, -1))
        z = bipolar(v)
        dz = dbipolar(z)
    
        r = d[i]-z
        
        delta = np.multiply(r, dz)
        dp = np.multiply(np.dot(delta, w[:,0:2]), dy)
        deltawp = n*np.dot(np.array([dp]).T, np.array([x[i]]))
    
        # Update weights
        w = w + n*np.dot(np.array([delta]).T, np.array([np.append(y, -1)]))
        wp = wp + deltawp
        
        # Update weights record
        wh.append(w)
        wph.append(wp)
        
        p = np.sum(0.5*(r**2))
        e += p
    cr.append(e)

Cycle error curve:

# Cyle Error curve
plt.rcParams['figure.figsize'] = [10, 6]
plt.style.use('ggplot')
fig, ax = plt.subplots()
ax.plot(range(len(cr)), cr,
       linestyle='--',
        color='blue')
ax.set_ylabel('Error')
ax.set_xlabel('Cycle')
ax.set_title('Cycle Error Curve')
plt.show()

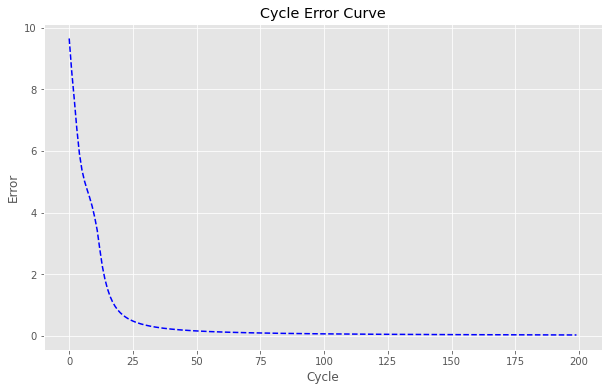
Prediction

The test character below, has the following feature input vector:

x1_2_fig = np.array([1,1,1,-1,-1,1,1,-1,-1,1,-1,-1,-1,1,1,-1])
x1_2 = np.array([1,1,1,-1,-1,1,1,-1,-1,1,-1,-1,-1,1,1,-1,-1])

plt.rcParams['figure.figsize'] = [5, 5]
plt.style.use('default')
fig, ax = plt.subplots()
ax.imshow(x1_2_fig.reshape(4,4))
plt.axis('off')
plt.title('Test Character')
plt.show()

With the current set of weigths, the new input image will be classified as a T with d = [1, -1, -1]

# Classification using final weights
vp = np.dot(wp, x1_2)
y = bipolar(vp)

v = np.dot(w, np.append(y, -1))
z = bipolar(v)
print(z)
print(np.round(z))

[ 0.9352934  -0.94743224 -0.95992767]
[ 1. -1. -1.]